1. Mechanisms
Concepts and terminology
A central issue of a digitally based analysis of data is the linearity vs. non-linearity of an argument. The very fact that a proper term is missing to refer to non-linearity suggests that the field remains wide open for a clarification of the issue. As a contribution in that direction, we should reflect on some key concepts, distinguishing between the form and the substance of the argument.While I suggest alternative positive terms (multi-linear, polyhedral) in lieu of the negative term "non-linear," I do nevertheless retain the term "non-linear" simply because, by virtue of its oppositional value to "linear" and on account of its popularity, it provides a more immediate understanding of what is meant – as long as one attempts, as I do here, to explain what this meaning is.
Back to top
Sequentiality
We must distinguish between the logic of an argument and the form in which it is presented. If we use the terms "linear" to refer to the modality, we may use the term "sequential" to refer to the substance, of the argument. We may thus say that the argument will always be sequential, regardless of whether the form it takes is linear or not.In the schematic rendering below, the intermediate steps a-b-c-d must be in that sequence for the argument to hold. In this representation, these intermediate steps are all on the same plane, which results in an aligned set of arrows. But the steps may straddle across planes, resulting in a multi-linear or multi-layered arrangement – where sequentiality remains nevertheless the rule.

Schematic representation of sequentiality within argument
Multi-layering
In most cases, an argument includes multiple layers or registers, interlocked with each other. In this respect an argument is not only linear, but multi-linear, with the various threads running parallel, and yet calling at the same time for cross-overs from one linear path to the other. Thus, in the schematic rendering below, A is the main register, which runs linearly from beginning to end, and B and C are secondary registers which overlap either wholly (C) or partly (only the central portion of B being relevant to A). The argument still flows sequentially, but with data and inferences drawn from multiple planes.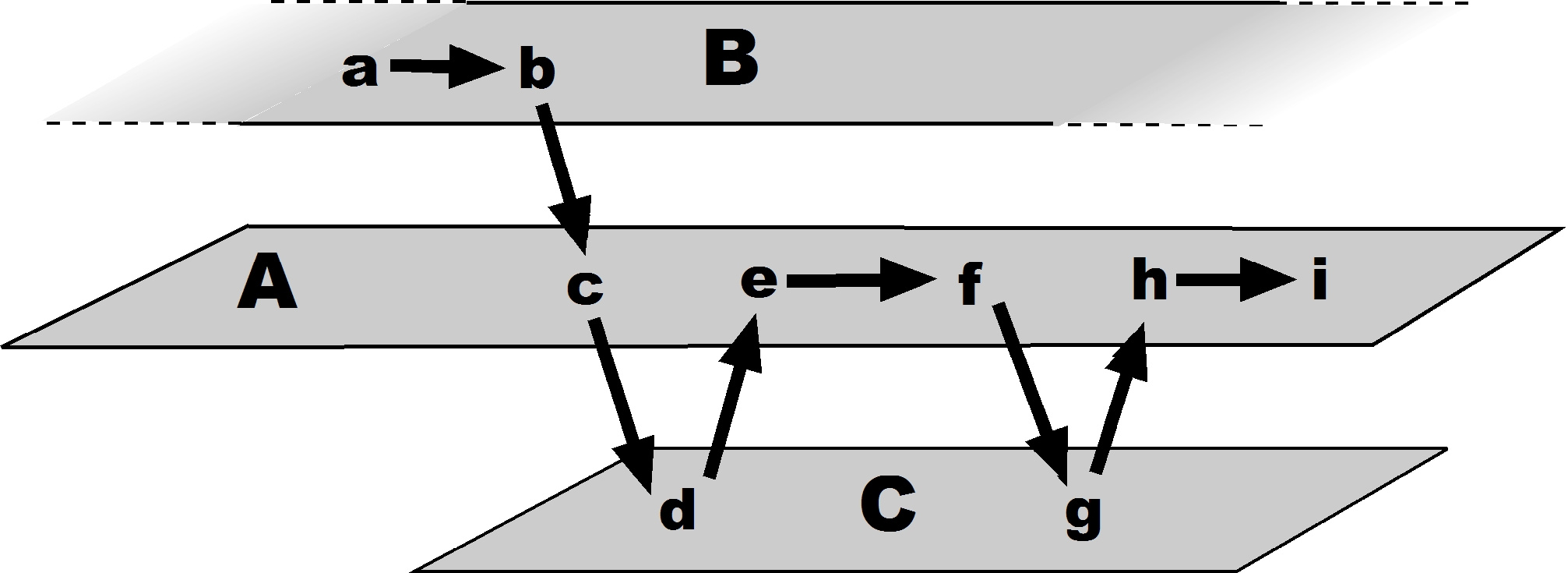
Schematic representation of a multi-layered argument
Reflection
|
The mechanisms described here help to understand what is the nature of reflection. To read in the sense of studying means more than being led passively along the sequential line proposed by the author. Rather, the reader is expected to develop parallel lines of inquiry and to draw on parallel data sets while following the argument presented by the author. There is, in other words, a parallel set of layers that the reader juxtaposes to those already offered by the author. This multi-linear function can be greatly enhanced when articulated digitally – which is precisely the great promise of the medium. Access to these multiple layers is dramatically facilitated by the medium, because of the way in which they are structured: there are unlimited lines of inquiry that are built on equally unlimited bodies of data. |

|
The non-linear, or multi-linear, perspective is interesting in that it shows both the positive and the negative aspects of the medium.
The positive side is that the bracketing of layers is practically unlimited, that a suggestion to explore a parallel layer can be elicited by explicit or implicit associative mechanisms (hyperlinks, search functions, etc.), and that within each layer one can pursue concomitant searches with the greatest of ease.
The negative side of things is that the very ease with which one can dart from one topic to the next, and within a topic from one detail to another, may deflect our attention and blind us to the reality of the initial goal. Instead of reflection, we then have distraction.
Back to top
2. Multi-linearity
The polyhedral argument
The adjective "linear" refers to the geometric figure of a line, i. e. a point moving along a fixed direction. The adjective "polyhedral" refers to the geometric figure of a solid bounded by polygons, such as the cube represented as 1 in the figure below. A linear argument that proposes to link conceptually points A and B has to travel along points c and d (2 in the figure). A polyhedral argument, on the other hand, travels directly, across the solid, from A to B (3 in the figure).The power and demonstrability of a polyhedral argument rely on a prior knowledge of the cube and of its properties. It is only in virtue of this knowledge that A can arguably be linked with B, since the whole structure of the cube is presupposed, hence the linear possibility of the link (as represented under 2) is virtually known, even if it is not followed. It is also as a result of the prior knowledge of the underly-ing structure (represented figuratively as a polyhedron) that the linkage takes place along the shortest line. Hence the power: greater prior knowledge allows the linkage. And hence the demonstrability: one can refer back to the nature of the solid and show how the link between the two is possible. Such a knowledge is "polyhedral" because it does not rely solely on points c and d, but rather on the whole solid figure (the cube or polyhedron), of which c and d are as much part as A and B.
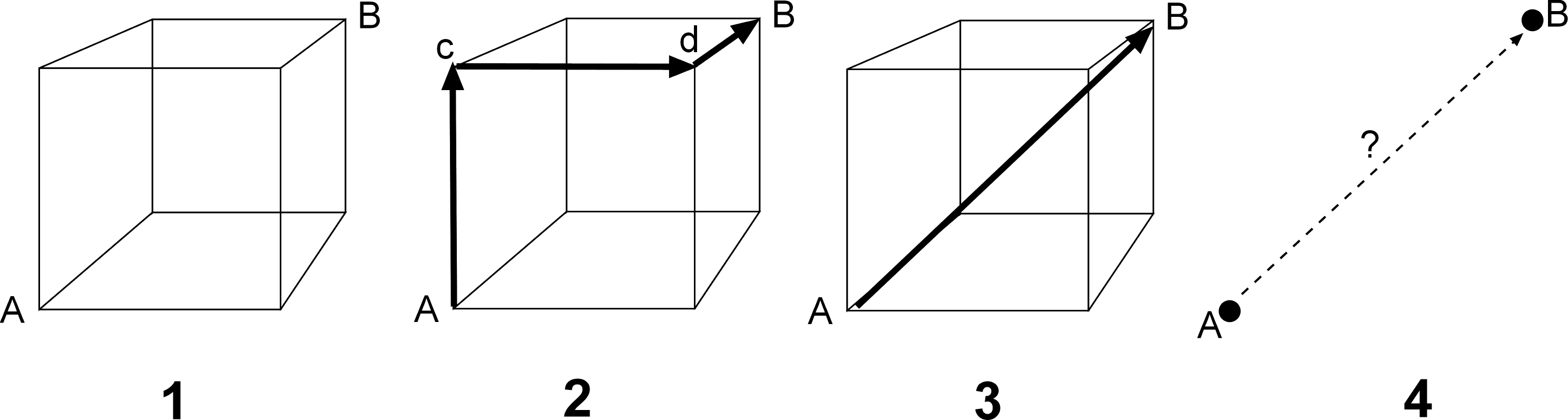
Without a supporting structure such as the cube, points A and B are floating in space, and their linkage (as shown schematically under 4 in the figure) results from a hit or miss shot in the dark.
Back to top
Linear and poly-segmental
It is further worth noting that, strictly speaking, even the linkage represented under 3 remains linear, since the linkage is indeed a line. To reflect properly the situation, the terms "poly-segmental" and "mono-segmental" are equivalent to "linear" and "non-linear." The argument's process represented under 2 is linear, but consists of many segments. The argument's process represented under 3, on the other hand, is also linear, but, as it cuts across the polyhedron in the most direct way, it consists of a single segment, and is therefore more effective. Obviously, the degree of effectiveness increases in proportion to the complexity of the structure.The Urkesh Global Record (UGR) is built in such a way as to allow precisely an extensive use of polyhedral arguments. In practice, this relies on systematic use of hyper-links, which are generated automatically and therefore in unlimited quantities. The arrow represented under 3 in Fig. 10-1 stands for such a hyperlink.
Back to top
Intuition
It is worth noting that the situation represented under 4 describes properly the nature of intuition. A connection between A and B may well be perceived through a sort of logical short-circuit, one that bypasses the argument and cannot therefore be demonstrated – at least, not on the basis of the original intuition. But we all know that in most cases it is precisely such an intuition that initiates the process of discovery. A proper polyhedral argument is one that, building on such an intuition, shows how the linkage is possible, and therefore arguable.Back to top
3. Non-digital multi-linearity
While non-linearity is typically associated with a digital format, the concept is by no means limited to it. There is a variety of other ways in which data can be displayed that respond to similar concerns (see also under Historical perspective).Back to top
Maps
A map organizes data in such a way that correlations among points are intuitively apparent through their two-dimensional layout. The links between these points (e.g., the direction of a travel line between two addresses, or the highlighting of differences in elevation between plains and mountains) can be construed as a non-linear argument. The map itself is not the argument, any more than a data base is, but the potentiality for explicit links makes the development of an argument quite more apparent than through a series of sequential statements.Back to top
Ledgers
See under historical perspective.Back to top
Graphic tabulation of data
The type of graphic design that translates complex data interrelationships into visually perceivable elements provides another important example of non-digital multi-linearity. A theory about the "visual display of quantitative information" was developed by Edward R. Tufte, and from the many examples gathered in his work one is led to reflect on the effectiveness of an argument developd in this way. The classic example of Charles Joseph Minard's graphic rendering of Napoleon's Russian campaign (Tufte 1983, pp. 40f and 176f), which is discussed in detail and which may "well be the best statistical graphic ever drawn" (p. 40), shows to the utmost how a non-digital, graphic multilinear argument can develop: a number of variables are interlaced in a coherent and cogent manner, and the perception of the whole is perfectly blended with the highlighting of the detail.Back to top
